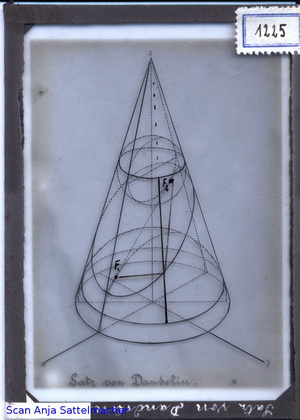
Diapositiv: Satz von Dandelin
Modell 1225
Beschreibung
Diapositiv: Satz von Dandelin über die Schnitte des Kreiskegels.
Ergänzungen
Das Diapositiv dient der Veranschaulichung des Satzes von Dandelin. Dieser besagt, dass beim Schnitt eines Kegels mit einer Ebene ein Kegelschnitt entsteht, wie man ihn durch eine Fadenkonstruktion erhält. Das heißt, dass der Schnitt eines Kegels mit einer Ebene, die nicht durch die Kegelspitze verläuft, ein regulärer Kegelschnitt ist.
Der belgische Mathematiker Germinal Pierre Dandelin (1794-1847) bewies diesen Satz, indem er, abhängig von der Lage der Ebene, ein bis zwei Kugeln definierte, die den Kegelmantel sowie die Ebene berühren. Die Punkte, in denen die sogenannten dandelin'schen Kugeln die Schnittebene berühren, sind die Brennpunkte $F_1$ und $F_2$ des jeweiligen Kegelschnitts.
Das Diapositiv zeigt dies am Beispiel der Ellipse.
Literatur
Hilbert, D.; Cohn-Vossen(1932). Anschauliche Geometrie, Springer-Verlag, Berlin. Online Version