Butenschöns Ellipsenzirkel

Dieser Ellipsenzirkel wurde hergestellt von Georg Butenschön’s Unternehmen für Messinstrumente. Der Zirkel sollte Handwerker, Techniker sowie Ingenieure bei ihrer Arbeit unterstützen. Dabei kann man Ellipsen in beliebiger Größe auf Papier, Holz, Glas mit Bleistift, Tinte, Tusche oder Diamant aufzeichnen.

Das Instrument besteht aus einem Führungskreuz, auf dem ein Maßstab mithilfe zweier Schlitten befestigt und bewegt werden kann. Der Maßstab wird mit Teilung nach oben in die beiden Schlitten eingeschoben. Es ist möglich, die beiden Halbachsen der gewünschten Ellipse festzulegen. Mit Hilfe aufgesteckter Veränderungsstücke lassen sich auch größere Ellipsen zeichnen. Ein Zeichengerät wird soweit in die dafür vorgesehene Bohrung des Maßstabes eingeführt, dass die Spitze leicht die Unterlage berührt. Hier spricht man von Papierstreifenkonstruktion (2. Art) als mathematischer Grundlage dieses Zirkels. Bei der Führung des Stiftes bewegt sich die Verbindungsstrecke zwischen beiden Markierungen auf den Schlitten (ein Endpunkt A und der innere Punkt B der Strecke $\overline{AP}$ ) auf zu einander senkrechten Kreuzarmen (zueinander senkrechten Geraden). Dabei beschreibt der Stift (der Endpunkt P) eine Ellipse.

Papierstreifenkonstruktion 2.Art
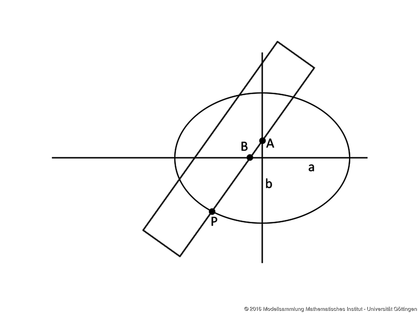
Bei dieser Konstruktionsvariante markiert man auf einem Streifen drei Punkte A, B und P mit Abmessungen $\overline{AP}=a$ (große Halbachse) und $\overline{BP}=b$ (kleine Halbachse), wobei der Punkt P nicht zwischen A und B liegt. Bewegt man den Streifen so, dass der Punkt B auf der Hauptachse der Ellipse und A auf der Nebenachse der Ellipse liegt, dann wandert der Punkt P auf einer Ellipse. Diese Konstruktion beruht auf dem folgenden Satz.

Bewegen sich ein Endpunkt und ein innerer Punkt einer Strecke auf zu einander senkrechten Geraden, so beschreibt der andere Endpunkt der Strecke eine Ellipse (vgl. Bild 2).

Text geschrieben von: Elena Bachmann